Méně je někdy více

Přečteš všechna slova?

A teď něco těžšího:
Me2d a me2dice měli v dou5i 2 medvíďata. Byli to bra3. Vyrostli z nich velcí lo3.
Jednou me2dice 8ahla na 100jacím vařiči ús3ce, pro které měli o2hu potá5 se jen kmo3 lachtani. Me2d si při100vil ke 100lku židli a ob1l si ještě o2r. Me2dí bra3 zatím pu100šili včelí úl. Přiletěl ptáček p8ěváček a řekl me2dovi, co může spa3t nedaleko v lese. Ten přestal dře5 na 100ličce a vydal se po 100pách. Malým nechyběla o2ha. Utekli přes bys3nu hluboko do lesa. Až pozdě večer šli z5 k me2dímu dou5i. Ale ne8ělili se při100upit. Me2dice zavě3ila a spa3la oba dře5 za keřem. Popadla je za kožich, oh0 přes koleno a odměnila je.
Me2dí rodiče na100lili přísný řád a od té doby pa3li bra3 k nejhodnějším me2dům.
Každé písmeno nás stojí energii k jeho zaznamenání. Energie můžeme ušetřit nějakým
vhodným zkrácením textu tak, aby smysl textu zůstal zachován. Můžeme využít opakujících se slov nebo částí slov a označit je nějakým kódem a pak kód použít místo slova nebo části slova.
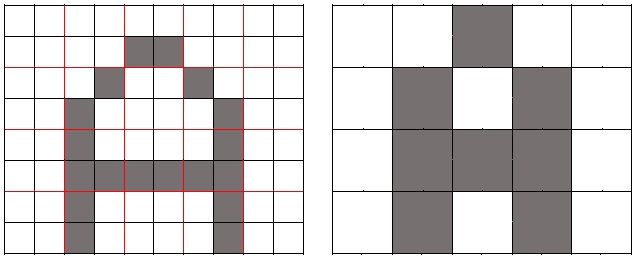
Opakující se slova nebo části slov můžeme znázornit i graficky:

Na každý pixel u rastrového obrázku potřebuje počítač nějakou velikost paměti. U každého si pamatuje informaci o jeho barvě. Když jsme kódovali (rastrový) obrázek, tak se stejně barevná pole shlukovala. Když na sebe úsečky u (vektorového) obrázku navazovaly, tak jsme vynechávali společný bod. Zmenšit počet pixelů a přesto zachovat aspoň zhruba tvar objektu můžeme tak, že sousedící pixely spojíme do jednoho s převažující barvou.
Čtyři pixely tvořící čtverec spojíme do tohoto jednoho většího čtverce. Otázkou pak je, jakou bude mít tento čtverec barvu.
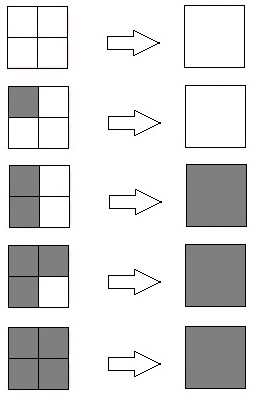
Pokud všechny malé čtverečky byly bílé, pak bude i ten nový velký bílý.
Bílý bude také, pokud z původních čtyř malých byl zabarvený maximálně jeden.
V ostatních případech bude mít velký čtverec barvu vybarvených polí. Také přirozeně platí, že čím méně rozlišuji v obrázku barev, tím zabírá méně místa.
Jak po dokončení přenosu dat z jednoho zařízení na druhé zjistí,
že obdrželo celý kód?
Přenosový kanál je vždy více či méně zašuměn.
Budou se nám tedy náhodně
měnit písmenka v textu
nebo barvy v obrázku?

Nebudou.
Chybám se sice nedá zabránit, dají se však pomocnými (nadbytečnými) daty a matematickými metodami opravit.
Kontrolní součty jsou v principu velmi jednoduché a přitom velmi účinné. Po určené skupině čísel vysílač spočítá jejich kontrolní součet a ten pošle přijímači.
Přijímač zná stejný algoritmus (postup) a také vždy po určené skupině čísel vypočítá jejich (kontrolní) součet a porovná ho se součtem, který mu došel od přijímače.
Tato metoda má hned dvě funkce (výhody), máme jistotu, že data byla dokonale přenesena a pokud malá část dat, vypadne, můžeme chybějící data dopočítat.
Zjednodušeni zápisu, kontrolní součet
Kvůli přenosu dat se snažíme o zmenšení jejich velikosti využíváním různých postupů.
Abychom měli jistotu, že data dorazila všechna, připojuje se tzv. kontrolní součet.
Kontrolní součet je doplňková informace, která se předává spolu s vlastní informací a slouží k ověření, zda je vlastní informace úplná a zda při jejím přenosu nedošlo k chybě. Kontrolní součet je výsledkem nějaké předem určené operace, provedené s vlastní informací.

Procvičujeme s Bobrem
Sada úloh se týká problémů při ZTRÁTĚ DAT během jejich přenosu, kontroly dat po přenosu a také ZMENŠENÍ MNOŽSTVÍ PŘENÁŠENÝCH DAT (kompresí).
Copied from: Informatika s BobříkemÚkol
Do pracovního sešitu pod nadpis zkopíruj text mezi čarami i obrázek.
Dekóduj zprávu, kterou poslala Ema.
Ze souboru Zjednodušení zkopíruj oba texty a podle zadání uprav (pod původní text zkopíruj text ještě jednou a ten uprav).
Do své prezentace do posledního obsahu dopiš název "Méně je někdy více".
Na konec prezentace vlož další snímek, napiš nadpis Méně je někdy více - kontrolní součet (písmo 24).
Na tento snímek zkopíruj poslední úkol a vyřeš ho, využij postupného doplňování a přepisování pomocí animace, při výpočtech můžeš použít kalkulačku.